RUDN University mathematician calculated the most effective vaccination strategy University
Within different groups of the population — for example, age or social — the epidemic spreads in different ways. Therefore, the overall rate of spread of the disease depends on the ratio of such groups in the population. The RUDN University mathematician, together with colleagues from India, Romania and France, built a mathematical model and found out how many people need to be vaccinated and how best to vaccinate. The calculations were carried out in a generalized form, so the results can be useful not only in the conditions of any epidemic or pandemic, including COVID-19.
“We studied a two-group epidemic model. The groups differ in the rate of transmission of the disease. Infection, the maximum and total number of infected depends on the ratio between the groups. We considered various strategies for distributing the vaccinated between the two groups and calculated what would be their outcome ”, - Doctor of Physical and Mathematical Sciences Vitaly Volpert, Director of the Interdisciplinary Research Center" Mathematical Modeling in Biomedicine “, RUDN University.
The model that mathematicians looked at describes two populations with different rates of infection and recovery. Mathematically, this model is expressed as a system of differential equations with four unknowns — the number of sick and healthy people in each of the two groups. The solution to these equations shows how many people in which group need to be vaccinated for the epidemic to subside. It is assumed that the vaccine itself is completely effective — after it it is impossible to get sick.
The results of the solution can be presented in the form of a graph — along the axes, the number of vaccinated in the first and second groups, and on the plane itself there is a closed figure: a triangle or a trapezoid. If the number of vaccinated in the first and second groups falls inside this figure, then the epidemic fades.
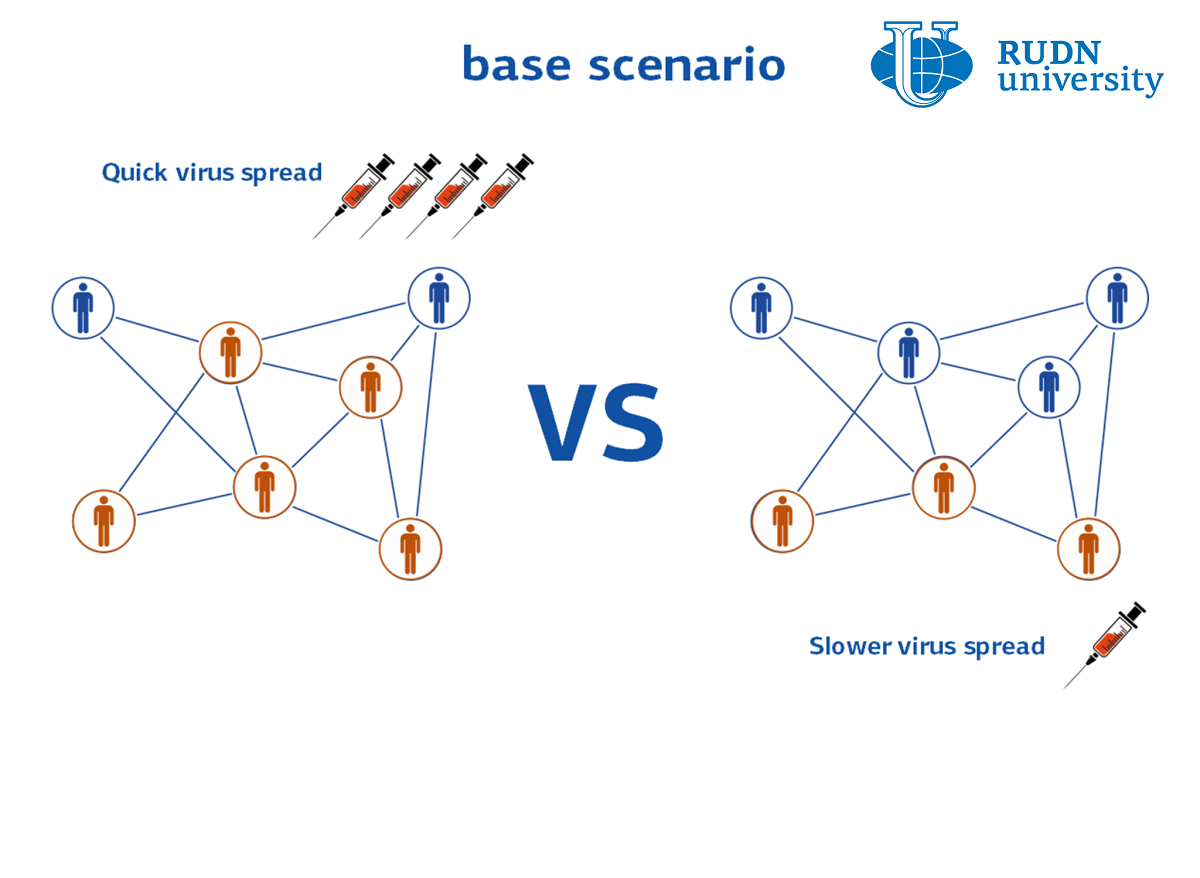
However, in real conditions, it is impossible to vaccinate the required number of people at once — vaccination is carried out in stages. This is due to both economic and social factors. In terms of mathematics, all these factors can be described in terms of the generalized “cost” of vaccination. To find out which vaccination strategy will be the most effective, the RUDN University mathematician solved the minimization problem — an integral equation that allows you to find the minimum of both the number of infected in each group and the cost of vaccination. Mathematicians tested four vaccination strategies. Each was carried out in five stages with the same total number of vaccines at each stage, but with a different ratio of vaccinated from the two groups. For all strategies, mathematicians determined how the total number of cases will change over time.
It turned out that the least effective strategy is “natural”, when people for vaccination are randomly selected evenly among the entire population. The following strategy turned out to be the most effective: at the first three stages, vaccinate approximately the same number of people from the group with a low infection rate and increase the number of vaccinated people from the second group several times, and vice versa at stages 4 and 5. These results are valid in the general case. However, depending on the characteristics of a particular disease, for example, with different mortality rates for different age groups, as in the case of COVID-19, the situation is reversed.
“In general, vaccination of the second group is more effective in terms of minimizing the number of infected. This conclusion could be expected since the rate of disease transmission in this group is higher. However, this conclusion may not be correct given the mortality in the two groups. Taking COVID-19 as an example, if we assume that the mortality rate among people over 60 is 10 times higher, then the total number of deaths decreases with a greater proportion of vaccinated in the first group, despite the fact that the infection rate in it is lower, ”- Dr. of Mathematical Sciences Vitaly Volpert, Director of the Interdisciplinary Scientific Center “Mathematical Modeling in Biomedicine” RUDN.
The results are published in the journal Applied Mathematics Letters.
On October 7–10, 2024 RUDN University Space Week traditionally took place. This event was dedicated to the World Space Week, which is celebrated annually in accordance with the UN General Assembly Resolution 54/68 (December 6, 1999) from October 4 to 10 to commemorate the launch of the first artificial satellite Sputnik-1 on October 4, 1957, and the signing of the Outer Space Treaty on October 10, 1967 – the fundamental international treaty in the field of international space law.
A RUDN agrotechnologist has identified wheat genotypes that are resistant to a dangerous fungal pathogen that infects plants even before the snow melts and reduces yields.
RUDN University engineers have calculated the parameters of a system that can prevent lunar power plants from overheating. These developments will be needed when planning for long-term lunar missions and colonizing the satellite.