RUDN mathematicians have created a method that can be used to study the properties of porous materials

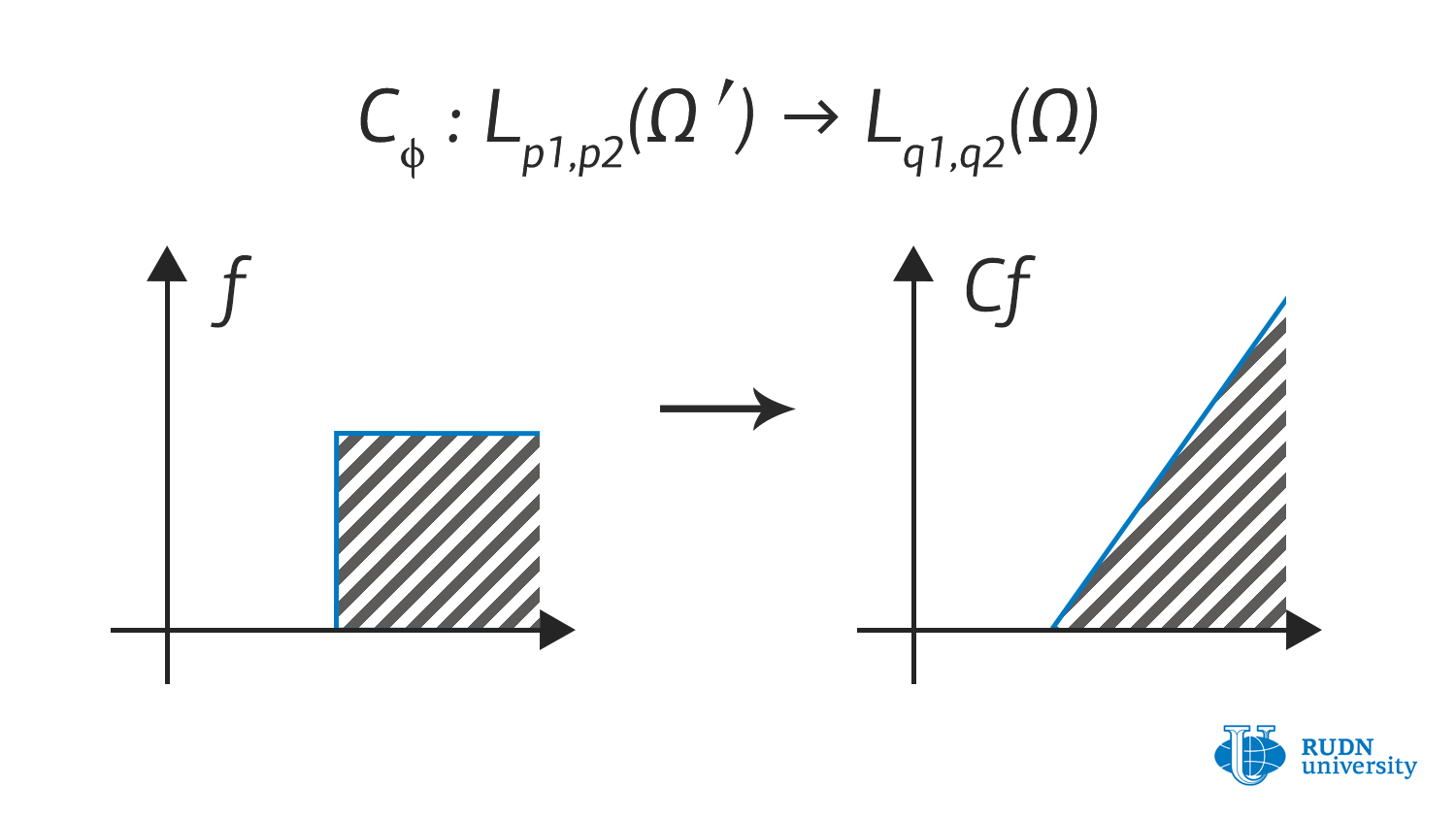
Just as any scientific and engineering field cannot exist without a theory, modern science of partial differential equations has its own “theory”-the language of functional analysis. Research of functional spaces in which solutions of equations are sought has been going on since the XIX century to our time. First, people learned to apply Fourier theory to solutions of the simplest linear partial differential equations, then they studied Banach and Hilbert spaces, as well as spaces of generalized functions — what is essentially the language of quantum mechanics.

Closer to the middle of the XX century, Sobolev spaces were discovered, which occupy one of the Central positions in the theory of partial differential equations. Over the next 50 years, they have been used to find many solutions to applications that are impossible to find in ordinary functional spaces.

Closer to the beginning of the XXI century, there was an urgent need for new methods for studying nonlinear partial differential equations — computational mathematics and the theory of integrable systems developed. However, the methods in these areas were too narrowly focused, and the need for language development has not disappeared.

Lebesgue spaces with mixed norms are more versatile and flexible in some situations. These spaces are defined as follows: we take the space of functions from several variables and define the norm as a repeated taking of the Lebesgue norm with two different parameters. They originally appeared as one of the generalizations of Lebesgue spaces, and have already attracted a lot of interest from theorists from several European countries, as well as China, Canada, and Russia.

Scientists from the RUDN Mathematical Institute Nikita Evseev and Alexander Menovschikov develop the theory of operators for such spaces, which allows them to be applied to applied problems formulated in the language of partial differential equations. They obtained a lot of new results describing the properties of operators on such spaces: criteria for operator bounding, properties of integral operators, multiplication operators, composition operators, and some others. They also obtained a number of auxiliary results that are useful for further development of this field.

“We believe that our methods and results can be applied for in evolutionary problems and differential problems on non-cylindrical domains. For example, in (mathematical) biology, where the studied surface or area changes over time, or in hydrodynamics for problems with a variable boundary,” says N. Evseev.

Developments in this area are useful for research on the Navier-Stokes equations , a system of equations describing Aero-and hydrodynamics. Lebesgue spaces with mixed norms allow evaluating solutions, which makes it possible, for example, to predict the absence of turbulence.

The obtained results also help to investigate applied problems of mathematical physics that arise in the study of porous materials and materials with cracks. For example, it will be possible to theoretically predict the pattern of diffusion and heat transfer in silicagels, porous glasses, various sponges and foams, as well as in some building materials.

Article in the Mathematical Notes.