The challenge of the Millennium. One step closer to the solution

The main purpose of the Navier-Stokes equations is to show how mathematics can be applied in practice in solving problems of modeling liquids and gases. For example, when modeling weather, ocean currents, air flow in a pipe or around an airplane wing. Since the 19th century, these equations have been used to describe the phenomena of the physical world. RUDN University scientists managed to significantly improve the quality of approximation of the numerical solution of a system of differential equations.

The Navier-Stokes equations (NSE) are a system of nonlinear partial differential equations. These are the most important equations in hydrodynamics: they are used for mathematical modeling of many natural phenomena and technical devices.

In the case of a mathematical model of a continuous medium-a viscous incompressible liquid, for example, water, the system includes an incompressibility equation, usually called the continuity equation. This is a linear partial differential equation, which is a mathematical formulation of the law of conservation of the total mass of the liquid involved in the process under study. The remaining equations of the NSE system are nonlinear equations and are a mathematical formulation of the law of conservation of momentum for the elements of the volume of a liquid during its flow. From these equations, it is convenient to find by numerical methods the distribution of flow velocities in the considered volume of liquid. Depending on the process under study, the fluid flow can be considered as one-dimensional, two-dimensional or three-dimensional. This means that the variables describing fluid dynamics, i.e. the spatial components of velocity and pressure, depend, respectively, on one, two or three spatial coordinates. In addition, for a non-stationary (unsteady) flow, all these variables also depend on time.

The analysis of finite-energy NSE solutions, namely, the rigorous proof of the existence of such solutions, is the essence of one of the six unsolved “Millennium problems” for which the clay Mathematical Institute has awarded a $ 1 million prize. It is necessary to prove or disprove the existence of a global error-free solution of the Cauchy problem for three-dimensional NSE, which has finite energy.

A General analytical solution of the NSE, both for spatial and plane flow, cannot be found due to non-linearity and strong dependence on initial and/or boundary conditions. It remains to solve the NSE by numerical methods, for which the differential equations must be approximated, i.e. consciously simplified, by discrete equations. But at the same time, the challenge remains the construction of such an approximation, which inherits at a discrete level, with a sufficiently high accuracy, not only all the conservation laws (momentum and mass) inherent in the UNS, but also all the mathematical consequences of these equations.

In their 2017 paper [1], our scientists used modern computer algebra to construct a new second-order precision difference scheme for 2-dimensional NSE. The scheme on the test example of the only known non-stationary exact solution of the NSE showed very good numerical behavior.

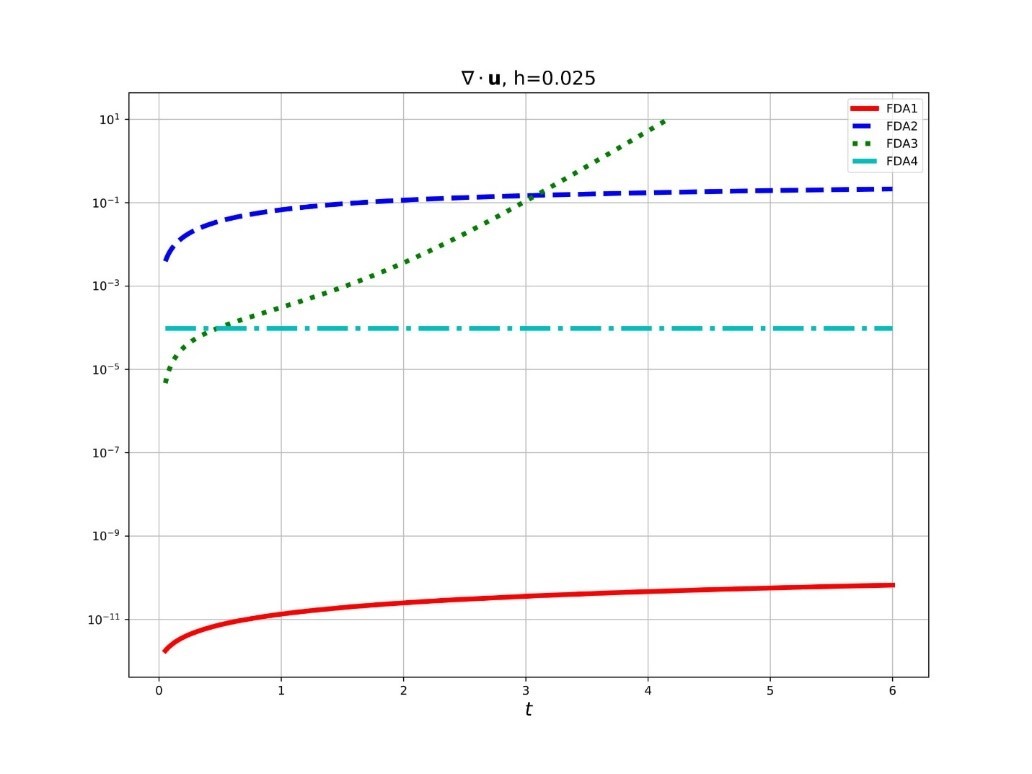
New numerical results obtained in the 2020 paper “Strong Consistency and Thomas Decomposition of Finite Difference Approximations to Systems of Partial Differential Equations” are shown in the figure below, where FDA1 is the described scheme and FDA2-FDA4 are the other schemes used for comparison. From the figure taken from the paper, it can be seen that the continuity equation is performed by the FDA1 scheme with an accuracy of 6 or more orders of magnitude higher than the accuracy of this equation by other explicit second-order schemes.

This accuracy of the continuity equation without its explicit consideration in solving the Cauchy problem is achieved for the first time and is an unprecedented result. In addition, the fda1 scheme is significantly superior (by 10 or more times) to the FDA2-FDA4 schemes, both in terms of the accuracy of calculating speeds and pressure.

1. P.Amodio, Yu.A.Blinkov, V.P.Gerdt and R.La Scala. Algebraic construction and numerical behavior of a new s-consistent difference scheme for the 2D Navier—Stokes equations. Appl. Math. Comput., 314 (2017), 408–421. 
2. V.P.Gerdt, D.Robertz and Yu.A.Blinkov. Strong Consistency and Thomas Decomposition of Finite Difference Approximations to Systems of Partial Differential Equations. arXiv:2009.01731 [cs.SC]. (2020), 47 p.

Millennium problems — in 2000, the Clay Mathematical Institute announced a list of the most important classical problems that have remained unanswered for many years. For solving each of the problems, now there are six of them, the clay Institute has appointed a prize of 1,000,000 US dollars. One of the Millennium problems (the Poincare hypothesis) was solved by the Russian mathematician G.Ya. Perelman in 2002-2003.

The Clay Mathematical Institute is a private Institute in the United States, founded in 1998. The main goal of the mathematical Institute is to increase and disseminate knowledge in the field of mathematics.

The Cauchy problem is one of the main problems of the theory of differential equations. It consists in finding a solution (integral) of a differential equation that satisfies the so-called initial conditions (initial data).