RUDN University mathematician first described the movement in a flat strip of plasma

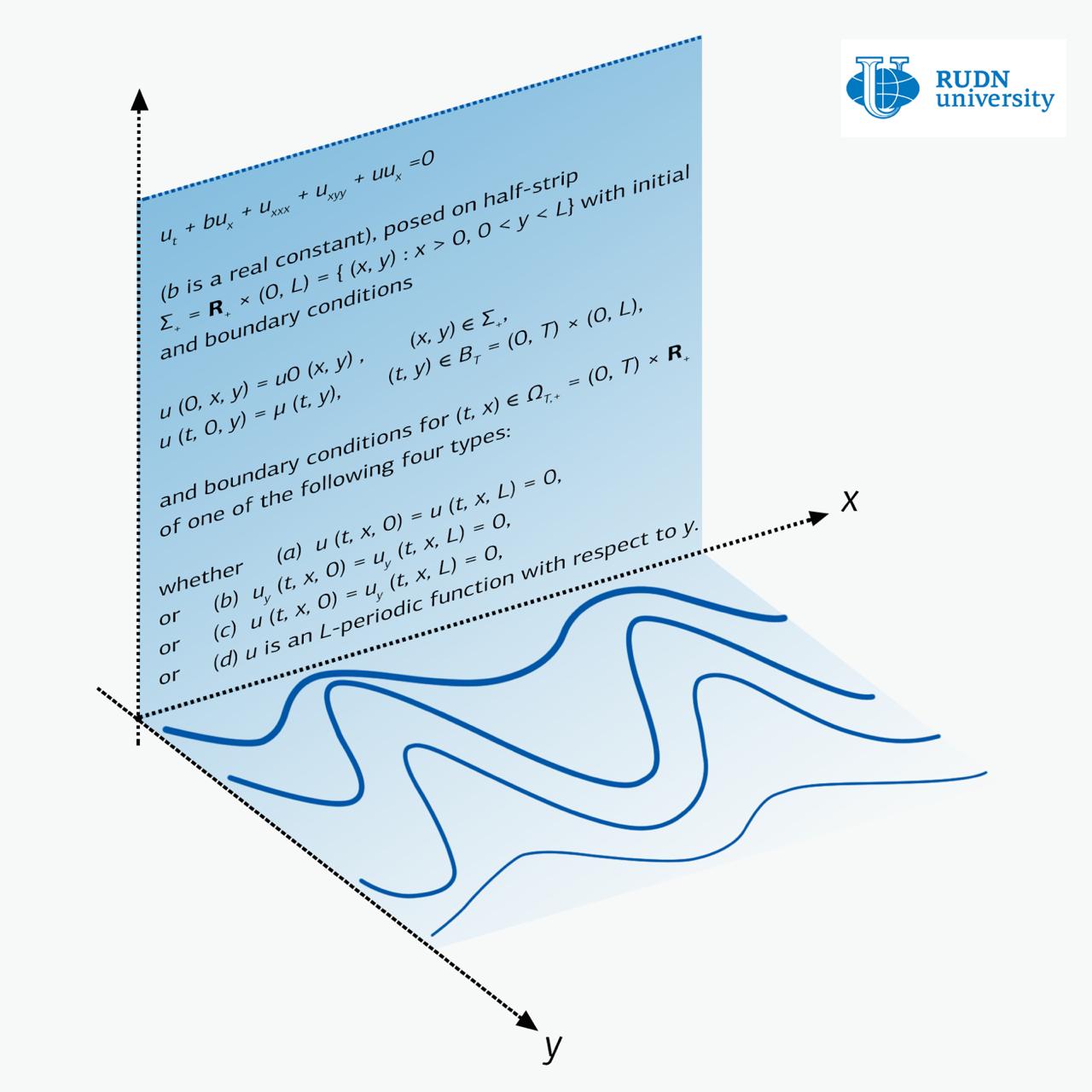
The Zakharov-Kuznetsov equation is a one-function equation of two variables x and y. For physics, x is the direction of wave propagation, and the deformation of the medium occurs along the perpendicular direction y. For example, an oscillation of the guitar string looks like the wave runs down the string, while the oscillations occur perpendicular direction relative to the run of the wave.

There are a large number of results that describe solutions of the Zakharov-Kuznetsov equations in the case when there are no constraints on y. But the question of wave propagation in the strip — when y is limited — was almost not studied until recently. And this is although such a statement of the problem has a physical meaning, and therefore potential applications.

RUDN University mathematicians dealt with the Zakharov-Kuznetsov equation in the strip. They examined three main cases — when there are no oscillations on the boundary of the strip, when there is no current on the same boundary and when the boundary conditions are periodic in structure. The latter case corresponds to the propagation of waves in a medium whose structure is periodic in x.

In all these cases mathematicians managed to prove theorems of existence and uniqueness of solutions. For systems of partial differential equations, which include the Zakharov-Kuznetsov equation, such equations are very rare.

These results are the first for solutions of the equation with initial conditions in the strip. Flat plasma flows with boundary conditions, which were considered by RUDN University scientists, can occur in physics and astrophysics.

The Zakharov-Kuznetsov equations belong to a wider category of equations known as the Korteweg-de Vries equations. In the study of this category of equations for the first time, it was possible to describe solitons — waves whose shape does not change during movement. Physicists consider solitons as a tool for modern optical data transmission systems. The study of solitons, which can arise in the Zakharov-Kuznetsov equations, is one of the options for the development of the work done by RUDN University mathematicians.

The article in the journal Nonlinear Analysis: Real World Applications